Traditional search methods work well when finding local solutions around a given starting point with model data that are precisely known. These methods fail, however, when searching for global solutions to real world problems that contain significant amounts of uncertainty. Recent developments in optimization have produced efficient search methods capable of finding optimal solutions to complex problems involving elements of uncertainty.
OptQuest incorporates metaheuristics to guide its search algorithm toward better solutions. This approach uses a form of adaptive memory to remember which solutions worked well before and recombines them into new, better solutions. Since this technique doesn’t use the hill-climbing approach of ordinary solvers, it does not get trapped in local solutions, and it does not get thrown off course by noisy (uncertain) model data. You can find more information on OptQuest’s search methodology in the publication references listed in the OptQuest section of the Oracle Crystal Ball Reference and Examples Guide.
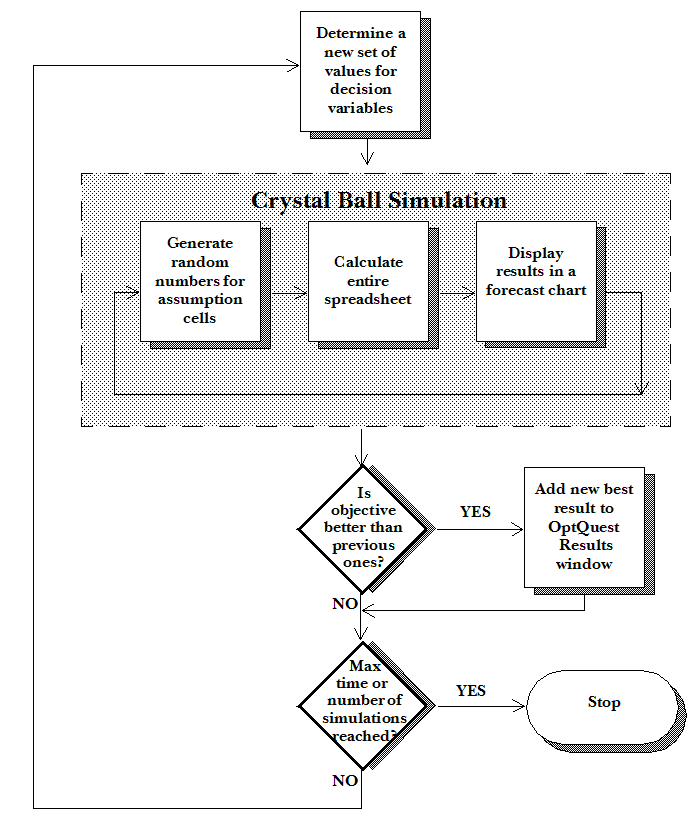
Once you describe an optimization problem (by selecting decision variables and the objective and possibly imposing constraints and requirements), OptQuest invokes Crystal Ball to evaluate the simulation model for different sets of decision variable values. OptQuest evaluates the statistical outputs from the simulation model, analyzes and integrates them with outputs from previous simulation runs, and determines a new set of values to evaluate. This is an iterative process that successively generates new sets of values. Not all of these values improve the objective, but over time this process provides a highly efficient trajectory to the best solutions.
As shown in the following flow chart, the search process continues until OptQuest reaches some termination criteria, either a limit on the amount of time devoted to the search or a maximum number of simulations.