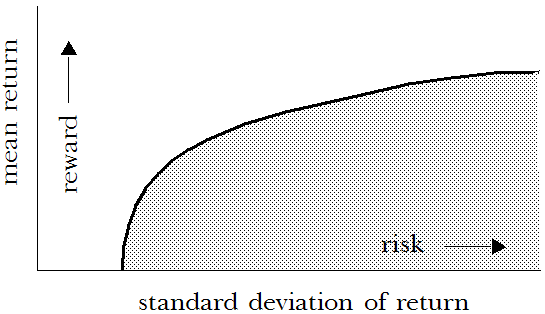
Si tuviera que examinar todas las combinaciones posibles de estrategias de inversión para los activos descritos para Portfolio Revisited.xls, observaría que cada cartera tiene un rendimiento medio determinado y una desviación estándar del rendimiento asociado. El trazado de las medias en un eje y las desviaciones estándar en otro, puede crear un gráfico como este:
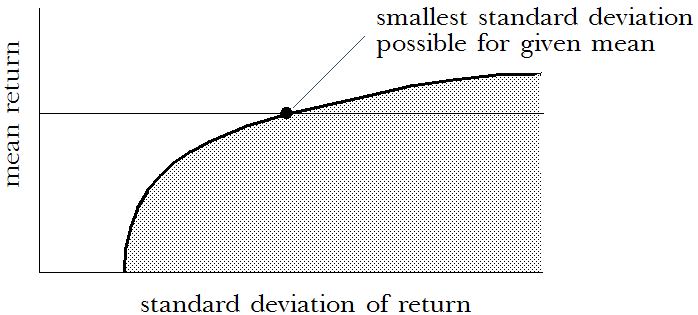
Los puntos en o por debajo la curva (valores menores que la curva) representan combinaciones posibles de inversiones. Los puntos por encima de la curva (valores mayores que la curva) son combinaciones que no se pueden obtener con el conjunto concreto de activos disponibles. Para cualquier rendimiento medio determinado, una cartera tiene la menor desviación estándar posible. Esta cartera se encuentra en la curva en el punto que interseca la media del rendimiento.
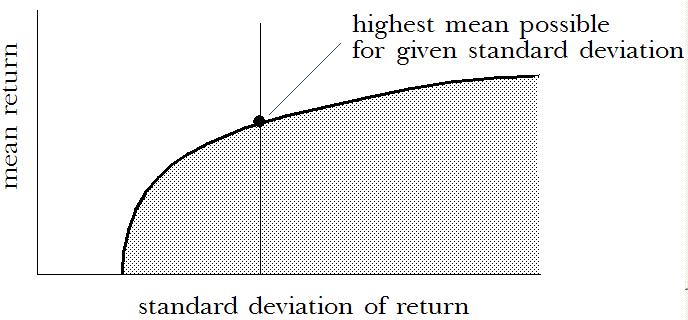
Igualmente, para una desviación estándar determinada del rendimiento, una cartera tiene el mayor rendimiento medio que se puede obtener. Esta cartera se encuentra en la curva en el punto que interseca la desviación estándar del rendimiento.
Las carteras que están directamente sobre la curva se denominan eficientes (consulte Markowitz, 1991 que se indica en las referencias de publicaciones de la sección de OptQuest de la guía de referencia y ejemplos de Oracle Crystal Ball), ya que es imposible obtener un rendimiento medio mayor sin generar mayores desviaciones estándar, o menores desviaciones estándar sin generar un rendimiento medio menor. La curva de carteras eficientes a menudo se denomina frontera eficiente.
Las carteras con valores menores que la curva se denominan ineficientes, lo que significa que existen mejores carteras con mayores rendimientos, menores desviaciones estándar o ambos.
En el ejemplo de Guía de aprendizaje 2: modelo de Portfolio Allocation se utiliza una técnica para buscar soluciones óptimas en la frontera eficiente. Este método utiliza la media y la desviación estándar de los rendimientos como criterios para equilibrar el riesgo y la recompensa.
También puede utilizar otros criterios para seleccionar carteras. En lugar de utilizar el rendimiento medio, puede seleccionar la mediana o modo como medida de tendencia central. Estos criterios de selección se llaman mediana-desviación estándar eficiente o modo-desviación estándar eficiente. En lugar de utilizar la desviación estándar de rendimiento, puede seleccionar la varianza, el mínimo de rango o el percentil de valor inferior como medida de riesgo o incertidumbre. Estos criterios de selección serán eficientes en sentido media-varianza, media-mínimo de rango o media-percentil.
El modo normalmente sólo está disponible para distribuciones de previsión con valores discretos donde los distintos valores se pueden producir más de una vez durante la simulación.