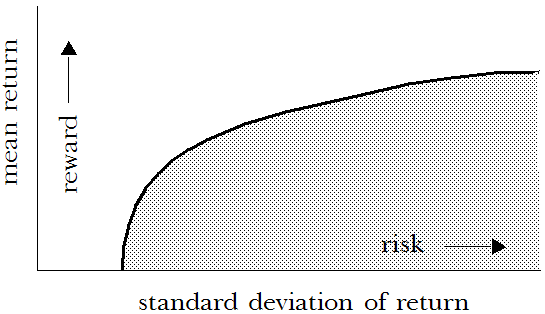
Si vous deviez examiner toutes les combinaisons possibles de stratégies d'investissement pour les immobilisations décrites pour le fichier Portfolio Revisited.xls, vous vous apercevriez que chaque portefeuille a une rentabilité moyenne qui lui est propre et un écart-type de rentabilité associé. Si vous représentez les moyennes sur un axe et les écarts-types sur un autre, vous pouvez créer un graphique semblable à celui présenté ci-dessous :
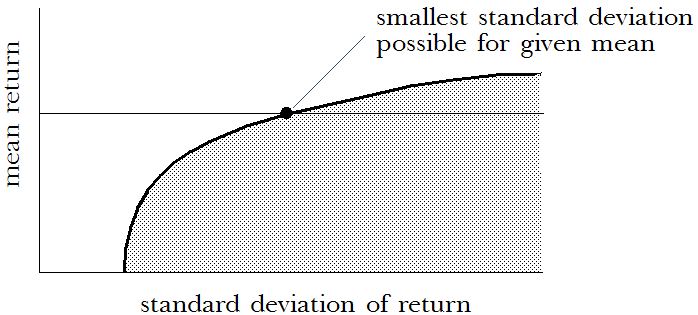
Les points situés sur ou sous la courbe (valeurs inférieures à la courbe) représentent les combinaisons d'investissements possibles. Les points situés au-dessus de la courbe (valeurs supérieures à la courbe) représentent des combinaisons inatteignables compte tenu de l'ensemble d'immobilisations particulier disponible. Un portefeuille dispose du plus petit écart-type possible pour chaque rentabilité moyenne donnée. Ce portefeuille se situe sur la courbe, au point de l'intersection avec la moyenne de la rentabilité.
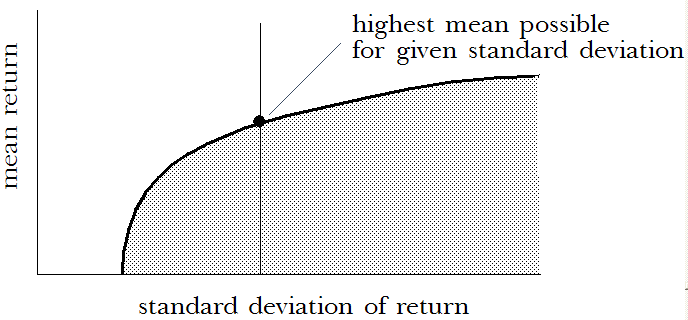
De la même façon, un portefeuille dispose de la plus importante rentabilité moyenne pouvant être obtenue pour chaque écart-type de rentabilité donné. Ce portefeuille se situe sur la courbe, au point de l'intersection avec l'écart-type de la rentabilité.
Les portefeuilles qui se trouvent directement sur la courbe sont dits efficients (reportez-vous à Markowitz, 1991 répertorié dans les références de publication de la section OptQuest du guide Oracle Crystal Ball Reference and Examples Guide, disponible en anglais uniquement) dans la mesure où il est impossible d'obtenir des rendements moyens supérieurs sans générer d'écarts-types supérieurs ou des écarts-types inférieurs sans générer de rendements moyens inférieurs. La courbe des portefeuilles efficients est souvent appelée frontière d'efficience.
Les portefeuilles dont les valeurs sont inférieures à la courbe sont dits inefficaces, ce qui signifie qu'il existe de meilleurs portefeuilles avec des rentabilités plus élevées, des écarts-types moins importants, ou les deux.
L'exemple de la section « Didacticiel 2 — Modèle Portfolio Allocation » utilise une technique donnée pour rechercher des solutions optimales sur la frontière d'efficience. Cette méthode emploie la moyenne et l'écart-type de la rentabilité comme critères pour équilibrer le risque et le gain possible.
Vous pouvez également utiliser d'autres critères pour sélectionner des portefeuilles. Au lieu de la rentabilité moyenne, vous pouvez sélectionner la médiane ou le mode comme mesure de la tendance centrale. Ces critères de sélection sont alors dits efficients du point de vue de l'écart-type/de la médiane ou de l'écart-type/du mode. Au lieu d'utiliser l'écart-type de la rentabilité, vous pouvez sélectionner la variance, la valeur minimale de la plage ou le fractile d'extrémité inférieure comme mesure du risque ou de l'incertitude. Ces critères de sélection sont dits efficients du point de vue de la variance/de la moyenne, de la valeur minimale de plage/de la moyenne ou du fractile/de la moyenne.
Le mode n'est en général disponible que pour les lois de prévision à valeur discrète où des valeurs distinctes peuvent exister plus d'une fois au cours de la simulation.