Suppose that you have recently purchased the Futura Apartments complex. One of your critical decisions is the amount of rent to charge. You have researched the situation and created a spreadsheet model to help you make a knowledgeable decision.
From the analysis of the price structures and occupancy rates of similar apartment complexes, you have estimated that demand for rental units is a linear function of the rent charged, and is expressed as:
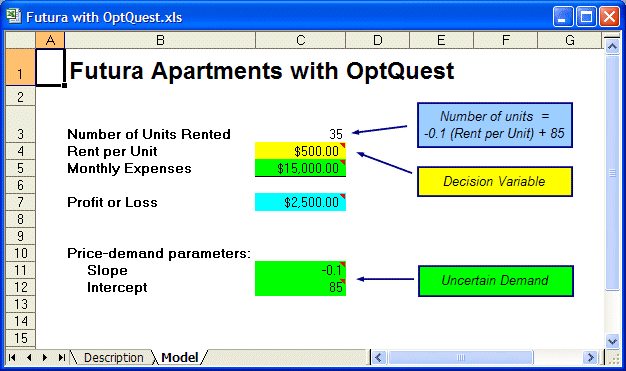
Number of units rented = -.1(rent per unit) + 85
for rents between $400 and $600.
In addition, you have estimated that operating costs will average about $15,000 per month for the entire complex.
You can use Predictor, supplied with Crystal Ball, to find the linear relationship of a dependent variable to one or more independent variables. |
 To begin the tutorial:
To begin the tutorial:
Open the Futura With OptQuest.xls workbook from the Crystal Ball Examples Guide (Figure 16, Futura Apartments Workbook).
Notice that the rent is set to $500, where:
Number of units rented = -.1(500) + 85 = 35
and the total profit will be $2,500. If all the data were certain, the optimal value for the rent could be found using a simple data table. However, in a more realistic situation, monthly operating costs and the price-demand function parameters (-.1 and 85) are not certain (probability distributions for these assumptions are already defined for this example). Therefore, determining the best rental price is not a straightforward exercise.
Before running OptQuest, select Run, and then Run Preferences and set the following run preferences: