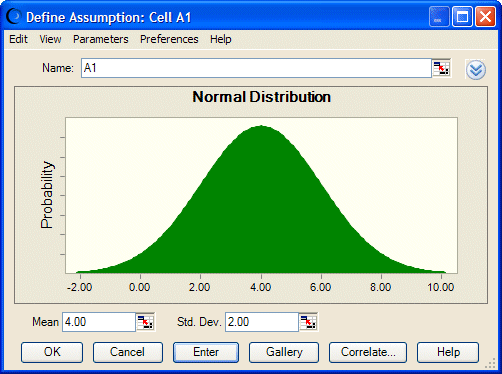
La distribución normal se puede utilizar para describir la inflación futura. Cree que la tasa más probable es del 4%. Está convencido de que la tasa de inflación podría tener la misma probabilidad de estar un 4% por encima como por debajo. También está seguro de que la tasa de inflación tiene un 68% de probabilidades de estar en algún punto dentro del 2% de la tasa del 4%. Es decir, que se calcula que hay aproximadamente una probabilidad de dos terceras partes de que la tasa de inflación estará entre 2% y 6%.
La distribución normal utiliza dos parámetros: Media y Desviación estándar. Ilustración 93 muestra los valores del ejemplo introducidos como parámetros de la distribución normal en Crystal Ball: una media de 0,04 (4%) y una desviación estándar de 0,02 (2%). La distribución muestra la probabilidad de que la tasa de inflación sea un porcentaje concreto.