En el ejemplo de análisis de la herramienta Simulación en 2D se utiliza un modelo de ejemplo de Crystal Ball, Toxic Waste Site.xls. Este modelo predice el riesgo de padecer cáncer en la población cercana a una instalación de residuos tóxicos. Esta hoja de cálculo tiene dos suposiciones de variabilidad y dos suposiciones de incertidumbre.
Para generar resultados, primero se establecen las preferencias de ejecución de Crystal Ball para la simulación Monte Carlo con la misma secuencia de números aleatorios y un valor de inicialización de 999. A continuación, la herramienta Simulación en 2D se ejecuta con la evaluación de riesgos (Risk Assessment) como previsión objetivo, el peso corporal (Body Weight) y el volumen de agua al día (Volume of Water per Day) en la lista Variabilidad del panel Tipos de suposición, así como la siguiente configuración de Opciones:
Al ejecutarse, la herramienta Simulación en 2D primero realiza una prueba de un solo paso para generar un nuevo conjunto de valores para las suposiciones de incertidumbre. A continuación, congela estas suposiciones y ejecuta una simulación de las suposiciones de variabilidad en el bucle interno.
La herramienta recupera la información de previsión de Crystal Ball después de ejecutar cada bucle interno. A continuación, la herramienta restablece la simulación y repite el proceso hasta que el bucle externo se ha ejecutado durante el número especificado de simulaciones.
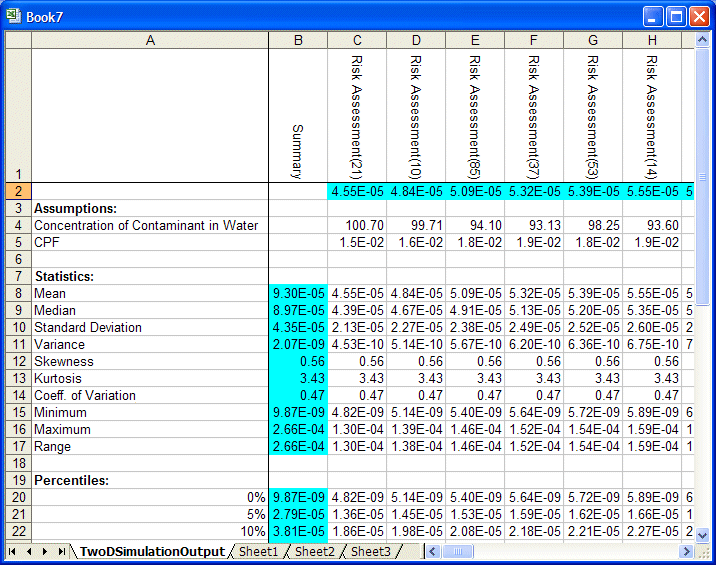
Los resultados de las simulaciones se muestran en una tabla que contiene las medias de previsión, los valores de suposición de incertidumbre y las estadísticas (incluidos los percentiles) de la distribución de previsión para cada simulación (Ilustración 68).
La herramienta también muestra los resultados de las simulaciones en dos dimensiones en un gráfico de superposición y un gráfico de tendencia.
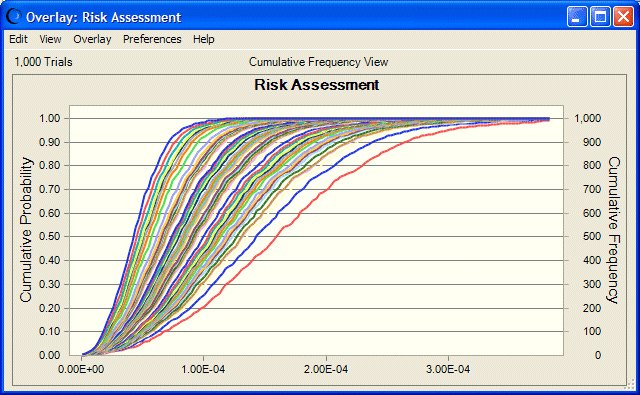
Las preferencias del gráfico de superposición se pueden establecer para que muestren las curvas de riesgo para las simulaciones de diferentes conjuntos de valores de suposición. Para ello, establezca la opción Tipo de gráfico de cada serie como Línea y seleccione la vista Frecuencia acumulada. Es conveniente utilizar las teclas de acceso rápido: Ctrl+t para el tipo de gráfico y Ctrl+d para la vista. Opcionalmente, utilice Ctrl+n para mover o eliminar la leyenda y Ctrl+m para recorrer las líneas de marcador de tendencia central.
Para este ejemplo, Ilustración 69 muestra que la mayoría de las curvas de riesgo se agrupan de forma densa hacia el centro, mientras que unas pocas curvas de valores atípicos se dispersan hacia el eje Frecuencia acumulada, en la que se mostrará la poca probabilidad de que haya un mayor riesgo.
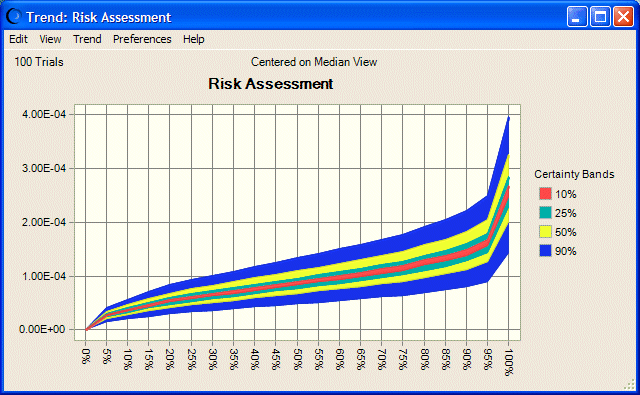
El gráfico de tendencia (Ilustración 70) muestra las bandas de certeza para los percentiles de las curvas de riesgo. El ancho de banda muestra la cantidad de incertidumbre en cada nivel de percentil para todas las distribuciones.
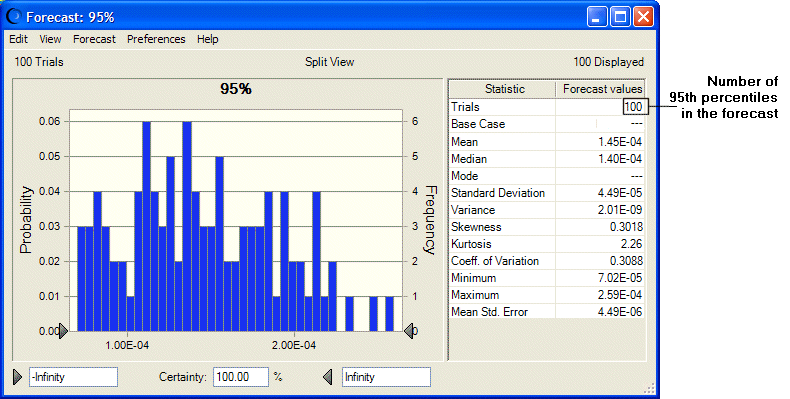
Puede centrarse en un determinado nivel de percentil, como el percentil 95, mediante la visualización de las estadísticas de previsión de percentil 95, que se muestran en Ilustración 71. Por ejemplo, en esta figura se muestran 100 pruebas, el número de percentiles 95 en la previsión.
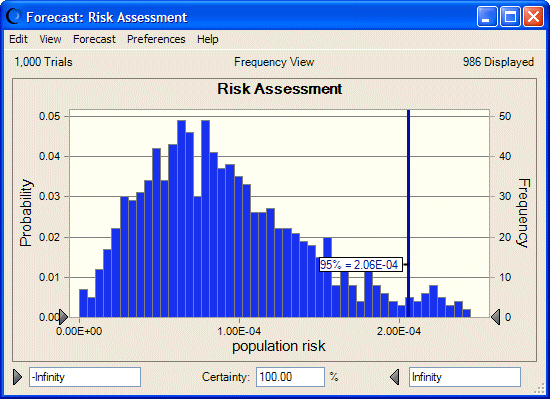
Compare los resultados de la simulación en dos dimensiones con la simulación en una sola dimensión (con tanto la incertidumbre como la variabilidad entremezclándose) del mismo modelo de riesgo, como en Ilustración 72.
La media de los percentiles 95 en Ilustración 71, 1,45E-4, es menor que el riesgo de percentil 95 de la simulación en una dimensión que aparece en Ilustración 72 en 2,06E-4. Esto indica la tendencia de los resultados de la simulación en una dimensión para sobrestimar el riesgo de población, especialmente para distribuciones muy sesgadas.
A menudo, los parámetros de suposiciones están correlacionados. Por ejemplo, correlacionaría una media mayor con una desviación estándar superior o una media inferior con una desviación estándar inferior. La definición de coeficientes de correlación entre distribuciones de parámetros puede aumentar la precisión de la simulación en dos dimensiones. Con los datos disponibles, como en los pesos corporales de muestra de una población, puede utilizar la herramienta Análisis de remuestreo para calcular las distribuciones de muestreo de los parámetros y las correlaciones entre ellos. |
Algunas suposiciones contienen elementos tanto de incertidumbre como de variabilidad. Por ejemplo, una suposición puede describir la distribución de los pesos corporales en una población, pero los parámetros de la distribución pueden ser inciertos. Estos tipos de suposiciones se denominan también suposiciones de segundo orden (también variables aleatorias de segundo; consulte Burmaster and Wilson, 1996, en la bibliografía). Puede modelar estos tipos de suposiciones en Crystal Ball colocando los parámetros inciertos de la distribución en celdas separadas y definir estas celdas como suposiciones. A continuación, puede vincular los parámetros de la suposición de variabilidad a las suposiciones de incertidumbre utilizando las referencias de celdas.
 Para ilustrar esto para la hoja de cálculo Toxic Waste Site.xls:
Para ilustrar esto para la hoja de cálculo Toxic Waste Site.xls:
Introduzca los valores 70 y 10 en las celdas G4 y G5, respectivamente.
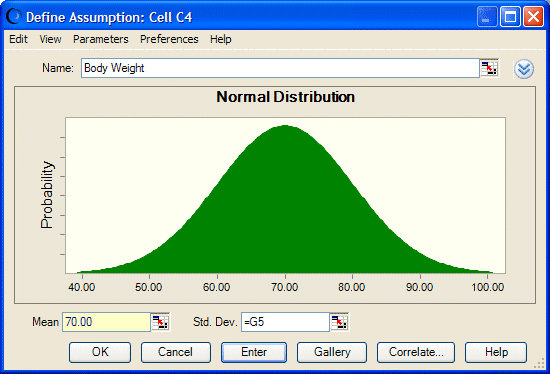
Se trata de la media y la desviación estándar de la suposición Body Weight en la celda C4, que se define como una distribución normal.
Define una suposición para la celda G4 con una distribución normal con una media de 70 y una desviación estándar de 2.
Define una suposición para la celda G5 con una distribución normal con una media de 10 y una desviación estándar de 1.
Introduzca las referencias a estas celdas en la suposición Body Weight (Ilustración 73).
Al ejecutar la herramienta para las suposiciones de segundo orden, se crea un modelo de la incertidumbre de los parámetros de suposiciones en la simulación exterior, y se crea un modelo de la distribución de la suposición (para diferentes conjuntos de parámetros) en la simulación interna.