L'exemple suivant d'analyse pour la simulation 2D utilise un modèle Crystal Ball intitulé Toxic Waste Site.xls. Ce modèle prévoit les risques de cancer pour la population riveraine d'une décharge de produits toxiques. Cette feuille de calcul contient deux hypothèses de dispersion et une hypothèse d'incertitude.
Pour générer des résultats, les préférences d'exécution de Crystal Ball sont tout d'abord définies pour la simulation de Monte Carlo de sorte à utiliser la même séquence de nombres aléatoires avec une valeur de départ de 999. L'outil de simulation est ensuite exécuté avec comme prévision cible "Risk Assessment". La liste Dispersion du volet Types d'hypothèse contient les facteurs "Body Weight" et "Volume of Water per Day", et les options suivantes sont définies :
Lors de son exécution, l'outil de simulation 2D effectue d'abord un tirage pas à pas afin de générer un nouvel ensemble de valeurs pour les hypothèses d'incertitude. Il fige ensuite ces hypothèses et exécute une simulation pour les hypothèses de dispersion dans la boucle interne.
L'outil extrait les informations de prévision de Crystal Ball après chaque exécution de boucle interne. Il réinitialise ensuite la simulation et répète le processus jusqu'à ce que la boucle externe ait été exécutée pour le nombre de simulations indiqué.
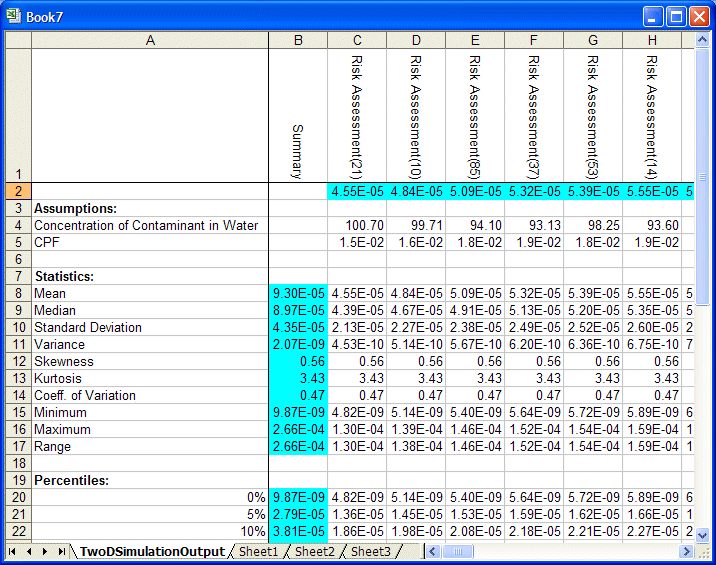
Les résultats des simulations sont affichés dans une table contenant les moyennes de prévision, les valeurs d'hypothèse d'incertitude et les statistiques (fractiles compris) de la loi de prévision pour chaque simulation (Figure 68).
L'outil trace également les résultats des dimensions des simulations 2D dans un graphique superposé et un graphique de tendance.
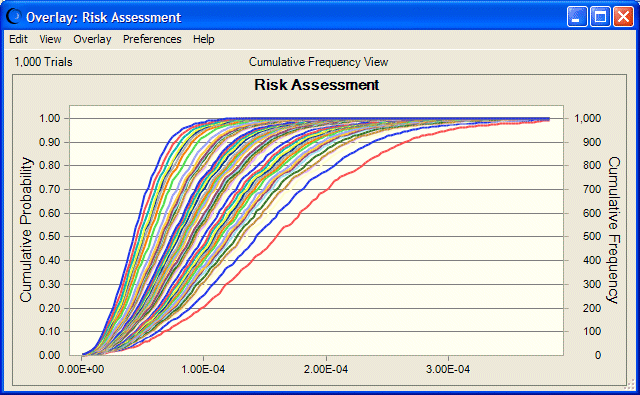
Vous pouvez définir les préférences du graphique superposé de sorte à afficher les courbes de risque des simulations pour différents ensembles de valeurs d'hypothèse d'incertitude. Pour ce faire, définissez le type de graphique de toutes les séries sur Ligne, puis sélectionnez la vue Effectif cumulé. Pour plus de commodité, servez-vous des raccourcis clavier : Ctrl+T pour le type de graphique et Ctrl+D pour la vue. Vous pouvez également appuyer sur les touches Ctrl+N pour déplacer ou supprimer la légende et sur les touches Ctrl+M pour faire défiler les lignes de marqueur de tendance centrale.
Dans cet exemple, la Figure 69 montre que la plupart des courbes de risque sont très regroupées vers le centre, alors que quelques courbes marginales sont éparpillées vers l'axe Effectif cumulé, ce qui traduit la faible probabilité d'un risque beaucoup plus grand.
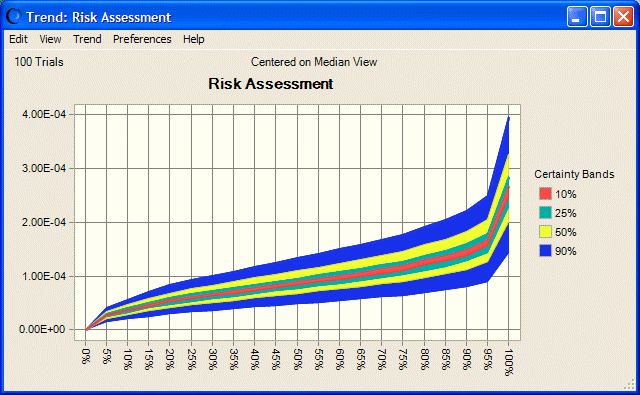
Le graphique de tendance (Figure 70) représente les bandes de certitude des fractiles des courbes de risque. La largeur de la bande indique le degré d'incertitude à chaque niveau de fractile pour toutes les lois.
Pour vous concentrer sur un niveau de fractile en particulier, tel que le 95e fractile, affichez les statistiques de prévision du 95e fractile, comme illustré par la Figure 71. Par exemple, cette figure représente 100 tirages, soit le nombre correspondant au 95e fractile de la prévision.
Comparez les résultats de la simulation bidimensionnelle à ceux d'une simulation unidimensionnelle (combinant incertitude et dispersion) pour le même modèle de risque, comme dans la Figure 72.
La moyenne du 95e fractile dans la Figure 71, 1,45E-4, est inférieure au risque du 95e fractile dans la simulation unidimensionnelle (2,06E-4), comme illustré par la Figure 72. Ceci indique que la simulation unidimensionnelle a tendance à surestimer le risque pour la population, en particulier pour les lois très asymétriques.
Les paramètres des hypothèses sont souvent mis en corrélation. Par exemple, vous pouvez mettre en corrélation une moyenne élevée et un écart-type élevé ou une moyenne faible et un écart-type faible. Le fait de définir des coefficients de corrélation entre les lois de paramètres permet d'accroître la précision de la simulation bidimensionnelle. Avec les données disponibles, comme un échantillon du poids de la population, vous pouvez utiliser l'outil d'amorce afin d'estimer les lois d'échantillonnage des paramètres et les corrélations entre elles. |
Certaines hypothèses contiennent à la fois des éléments d'incertitude et de dispersion. Par exemple, une hypothèse peut décrire la loi du poids des personnes au sein d'une population, mais les paramètres de la loi peuvent être incertains. On appelle alors les hypothèses de ce type des hypothèses de second ordre (ou variables aléatoires de second ordre ; voir Burmaster et Wilson, 1996, dans la bibliographie). Pour modéliser ces hypothèses dans Crystal Ball, placez les paramètres incertains de la loi dans des cellules distinctes et définissez ces cellules en tant qu'hypothèses. Ensuite, vous liez les paramètres de la loi de dispersion aux hypothèses d'incertitude à l'aide de références à des cellules.
 Pour illustrer ce propos dans la feuille de calcul Toxic Waste Site.xls, procédez comme suit :
Pour illustrer ce propos dans la feuille de calcul Toxic Waste Site.xls, procédez comme suit :
Saisissez les valeurs 70 et 10 dans les cellules G4 et G5, respectivement.
Il s'agit de la moyenne et de l'écart-type de l'hypothèse "Body Weight" dans la cellule C4, définie en tant que loi normale.
Indiquez une hypothèse pour la cellule G4 à l'aide d'une loi normale dont la moyenne est 70 et l'écart-type 2.
Indiquez une hypothèse pour la cellule G5 à l'aide d'une loi normale dont la moyenne est 10 et l'écart-type 1.
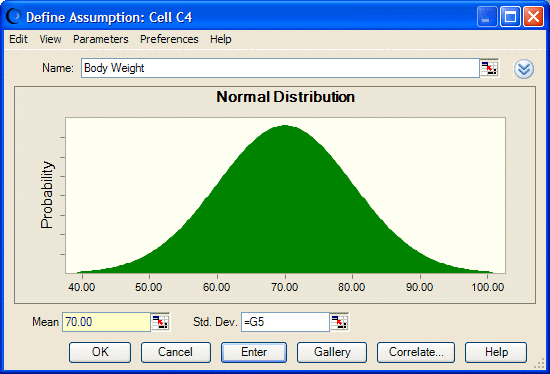
Entrez des références à ces cellules dans l'hypothèse "Body Weight" (Figure 73).
Lorsque vous exécutez l'outil pour des hypothèses de second ordre, l'incertitude des paramètres de ces hypothèses est modélisée dans la simulation externe, et la loi même de l'hypothèse est modélisée (pour différents ensembles de paramètres) dans la simulation interne.