 A detailed comparison of the top Monte-Carlo Simulation Tools for Microsoft Excel
A detailed comparison of the top Monte-Carlo Simulation Tools for Microsoft Excel
There are very few performance comparisons available when considering the acquisition of an Excel-based Monte Carlo solution. It is with this in mind and a bit of intellectual curiosity that we decided to evaluate Oracle Crystal Ball, Palisade @Risk, Vose ModelRisk and Frontline Risk Solver in terms of speed, accuracy and precision. We ran over 20 individual tests and 64 million trials to prepare comprehensive comparison of the top Monte-Carlo Tools.
Introduction
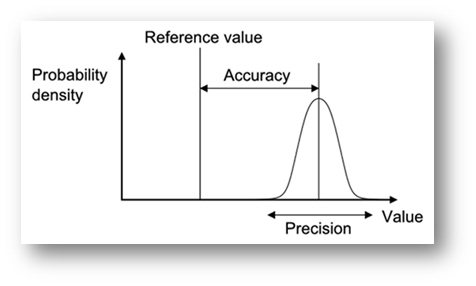
Figure 1: Precision Vs. Accuracy (source: http://en.wikipedia.org/wiki/Accuracy_and_precision)
|
In this article, we are going to cover an aspect of Monte Carlo tools which we are sure will be of interest to many – speed, accuracy and precision. Purely by accident, our curiosity was piqued when we ran several simulations and noticed that the standard deviation was moving around at certain percentiles at different rates than others. Therefore, we started wondering how much volatility would naturally occur at various percentiles across different packages.Our testing focused on two different aspects: accuracy and precision. We used the correlated returns model from our previous article as our test model. We ran the model 20 times at 10 000, 50 000 and 100 000 trials, resulting in 60 simulations per package. Furthermore, we ran three sets of tests, each of which removed an element that could throw the results off. The first test consisted of fitting data that had been generated using a Monte Carlo tool. The second test consisted of fitting data from actual data to eliminate fitting error that could potentially arise from using simulated data. The third test used normal distributions for all the assets in order to completely eliminate potential fitting error and put all the applications on the same footing.
In order to test for accuracy we averaged out the values of all 20 simulations for each percentile/package and compared the results against the calculated form using the Markowitz mean variance approach. As for precision, we looked at the standard deviation of each percentile/package at a given number of trials for all 20 simulations. For example, we would look at the standard deviation at the 99th percentile using a sample of 20 simulations at 10,000 trials each (200,000 trials total).
Our basic objective when analyzing a package for precision is whether it follows a certain set of statistical rules. A good example would be the expectation for a reduction of standard deviation as we increase the number of trials at a given percentile. When we set up the script to test the accuracy of each tool we realized that it would be easy to do a performance comparison as well. This turned out to be an added bonus! During the scripted tests, we also took into account the execution time of the whole script and that of each simulation. We also evaluated the average trials/sec for both the test and the individual simulations.
Tests and Analysis
Test Environment
Our test machine consisted of a Dell Dimensions XPS system with a 3.2 GHz dual core Pentium D, 4 GB of RAM, Windows XP and Microsoft Office 2010
Our Test Model
We are an investor that seeks to evaluate the risk in his portfolio. We have $250,000 to invest and we would like to make sure we have a better chance at making money than losing it. For purposes of the exercise, we have allocated our investment equally among each asset class at 25% a piece. We analyzed the rank correlation (using the Excel based method presented Copulas vs. Correlation) and prepared a correlation matrix that was used to correlate the returns distributions for each class. Please refer to our previous article on correlating distributions where we have prepared a video on how to do this with each package.
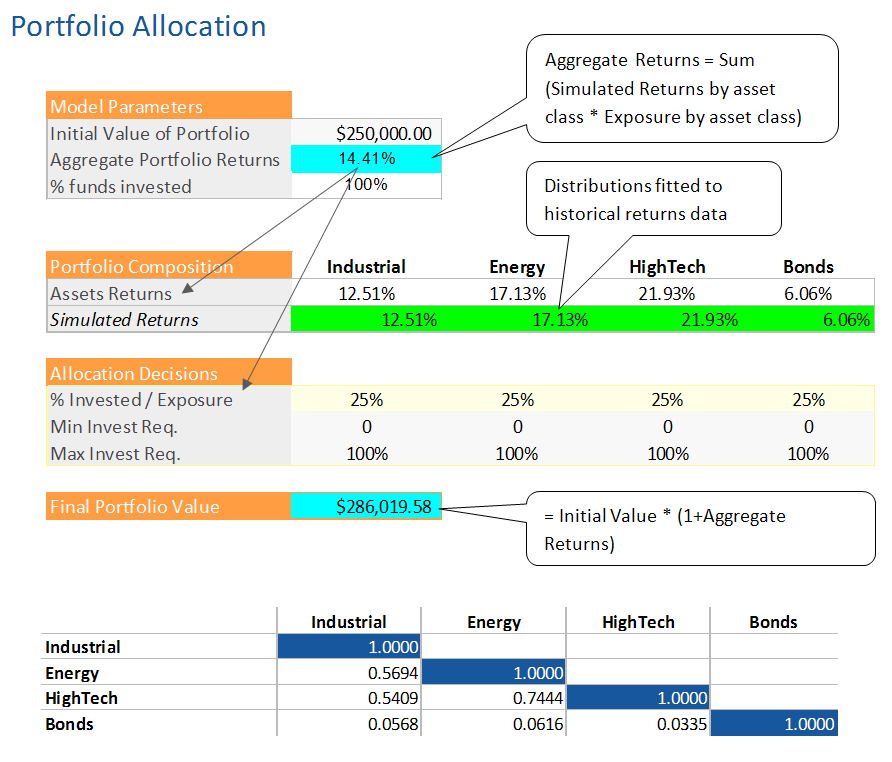
Since the applications fit the data using mostly normal distributions, we chose to use the Markowitz mean variance optimization method as a benchmark for the results at various numbers of trials (10k, 50k, and 100k).
With the Markowitz benchmarking data in hand, the first thing to do is contrast correlated versus uncorrelated results.
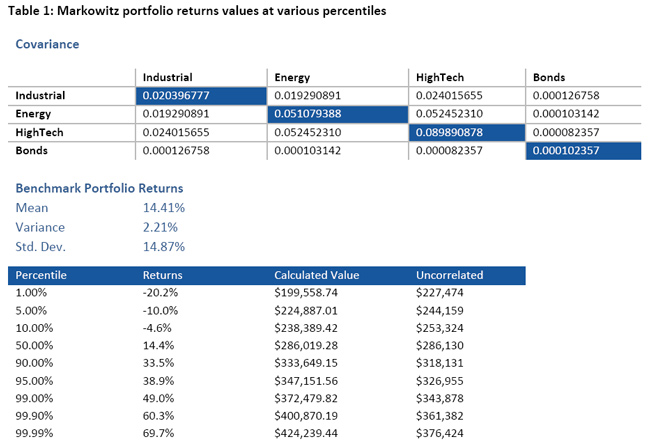
Clearly, the difference between the correlated and uncorrelated percentile values increases as we move away from the 50th percentile or Median. If we run this model without taking into account the correlation, we would be underestimating both the lower bound (loss) by almost 30 000$ and the upper bound by almost 50 000$. The consequence is that we are making decisions on the wrong range and risk profile – which could potentially be very good but mostly very bad because we are underestimating the downside risk.
The impact of correlation on the results
We ran each test with correlation turned on and off on all packages and tracked the results. This enabled us to both look at the results and the performance differences when handling correlation. The initial test was run only once with the correlation turned on while the two tests were run with it both on and off.
Curious about the results? Download Full Article and Test Results
Download the complete ZIP File. Read our comprehensive white paper analyzing the test results as well as the complete set of test results in Excel for slicing and dicing.
