 As stated in my last post, there are three common approaches to performing Tolerance Analysis. Let us describe the simplest of the three, the Worst Case Analysis (WCA) approach. An engineering-centric term in the Tolerance Analysis world would be Tolerance Stacks, usually meaning in a one-dimensional sense. The explanation begins with probably the most overworked example found in dusty tomes (my apologies in advance).
As stated in my last post, there are three common approaches to performing Tolerance Analysis. Let us describe the simplest of the three, the Worst Case Analysis (WCA) approach. An engineering-centric term in the Tolerance Analysis world would be Tolerance Stacks, usually meaning in a one-dimensional sense. The explanation begins with probably the most overworked example found in dusty tomes (my apologies in advance).
(I would like acknowledge James Ministrelli, DFSS Master Black Belt and GD&T Guru Extraordinaire, for his help & advice in these posts. Thanks, Jim!)
Examine Figure 2-1. There are four parts in this assembly. There is one part with a squared-off, U-shaped cavity in the middle. In that cavity will sit three blocks of the same width (at least they are designed that way). Those blocks were designed to fit side-by-side in contact with each other and within the cavity of the larger part. The intent is that they will "stack up" against the side of the cavity, thus leaving a designed gap on the other side. This designed gap has functional requirements (being part of a greater assembly) and, for proper operation, the gap size must be such-and-such-a-value with an allowable variation of such-and-such-a-value.
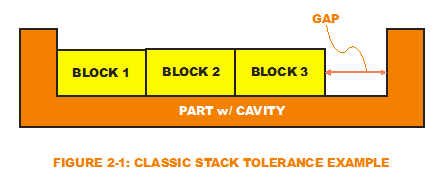 How would the designer determine what variation can be allowed on the widths (blocks and cavity) to ensure the gap variation meets the requirements? In WCA, a one-dimensional stack analysis would look at the extreme values allowed on the individual dimensions that would then "stack up" to be either the smallest possible gap or the largest possible gap. If those WCA values are within the desired system gap limits, then we are good to go. If not, what normally follows is a series of "what-ifs" where the individual tolerance values, perhaps even the nominal values they are controlling, are tinkered with until a winning combination is discovered that places the WCA values within the gap dimension requirements.
How would the designer determine what variation can be allowed on the widths (blocks and cavity) to ensure the gap variation meets the requirements? In WCA, a one-dimensional stack analysis would look at the extreme values allowed on the individual dimensions that would then "stack up" to be either the smallest possible gap or the largest possible gap. If those WCA values are within the desired system gap limits, then we are good to go. If not, what normally follows is a series of "what-ifs" where the individual tolerance values, perhaps even the nominal values they are controlling, are tinkered with until a winning combination is discovered that places the WCA values within the gap dimension requirements.
T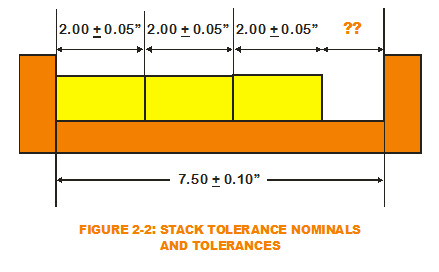 he biggest gap possible occurs when each of the individual block widths are at their smallest possible value and the width of the cavity is at its largest. For the block and cavity widths, this would correspond to the Least Material Condition. (LMC: The condition in which a feature of size contains the least amount of material everywhere within the stated limits of size.) All external features like widths are at their largest limit and all internal features like holes diameters are at their smallest limit under LMC.
he biggest gap possible occurs when each of the individual block widths are at their smallest possible value and the width of the cavity is at its largest. For the block and cavity widths, this would correspond to the Least Material Condition. (LMC: The condition in which a feature of size contains the least amount of material everywhere within the stated limits of size.) All external features like widths are at their largest limit and all internal features like holes diameters are at their smallest limit under LMC.
The smallest gap possible occurs when these same dimensions are at the opposite limits for Maximum Material Condition (MMC). LMC and MMC are important conditions when calculating dimensional WCA values. Below is a summary of the LMC and MMC dimension calculations and the resulting WCA values for the gap:
The process of tinkering with individual part tolerances, based on what the system variation goal is, termed Tolerance Allocation. (Another appropriate term is "Roll-Down" analysis, in that variance rolls down from system output and assigns allowable variation into the inputs.) There is an overall amount of variation allowed at the system level requirement (the gap) which is split into contributors at the individual part dimensions. Think of the overall variation as a pie that must be split into edible slices. Each slice then represents a portion of the pie that is allocated to each individual dimension so that the overall system level value variation is maintained within allowable limits.
In my next post, I will expound more on the Worst Case Analysis approach and introduce the concept of a transfer function. We will use transfer functions to calculate WCA extreme values, as well as for the other approaches still on the radar.
Creveling, Clyde M., Tolerance Design: A Handbook for Developing Optimal Specifications (1997); Addison Wesley Longman, pp. 105-111.
Sleeper, Andrew D., Design for Six Sigma Statistics (2006); McGraw-Hill, pp. 690-692, 704-707.