Let the battle begin anew. We continue our journey in uncertainty modeling, having understood how to fit distributions to data using Crystal Ball (CB). How does that experience compare to what ModelRisk (MR) has to offer?

Open the Duke 09_10 Scores spreadsheet with ModelRisk loaded in the Excel environment. We will first create the MR Objects representing the fitted PDFs. (Just as with the CB exercise, it is good practice to examine a variety of best-fitting distributions, rather than blindly accepting the top dog.) Then, in distinctly separate cells, we will create the VoseSimulate functions that behave as sampled values from the PDFs modeled by the MR Objects.

•  Select "Fit" button in the ModelRisk ribbon bar. (This opens the Distribution Fitting window. It does not matter which cell has been selected before clicking "Fit" button.)
• Select "Distribution Fit" in the drop-down list.
• Identify the "Data Location:" (upper left-hand corner) as Cells C4:C37.

 

• Select "Add" button (just below "Data location:" and "Truncated" enable box). (The PDF selection window will appear; see Fig. 4-1.)
• Select "Discrete" within "Type of Distribution" list (left-hand side).
• Individually select the first 11 distributions using CTL key.
• Select double right arrow (">>") button to place the identified distributions into right-hand column list.
• Select "OK."

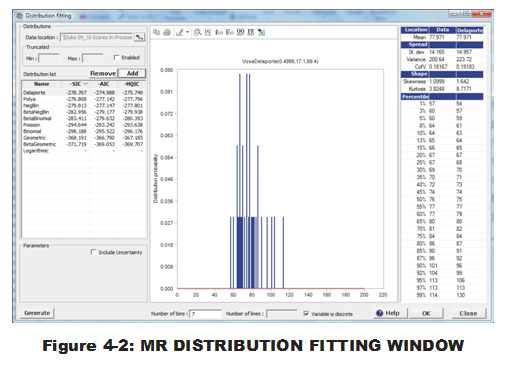
What appears next will be the user-friendly distribution-fitting window for MR with ranked distributions listed on the left-hand side (see Fig. 4-2). On the left-hand side are the distributions selected for fitting. They are ranked from top-to-bottom in order of best fits. Note that the criteria (SIC, AIC and HQIC) are not the same as used in CB (Chi-squared). And for good reason. These criteria penalize some fits as being less worthy if more parameters are used for the fitting. Just like with regression or ANOVA work, additional terms can be added for a better fit but that is a reflection of, perhaps, an unnecessarily-complex model. Simpler is better in many cases. Even with "over-fitting" penalties, the top-most distributions have two or more parameters, indicating the greater flexibility is desirable.

Now we will place both the MR Object and the PDF parameters into the spreadsheet.

• Select first distribution listed on left-hand side ("Delaporte").
• Select 'Excel-with-plus-sign' (right-most) icon above the histogram.
• Select "Parameters" from drop-down menu.
• Select Cells R4:T5.
• Select "OK." (These steps place the PDF parameters into the designated cells.)
• Select 'Excel-with-plus-sign' icon (again) above the histogram.
• Select "Object" from drop-down menu.
• Select Cell U5.
• Select "OK." (These steps place the MR Object into the designated cell.)

Of interest are the next four best-fitting distributions. Follow the same steps above for the next four PDFs. Before selecting the 'Excel-with-plus-sign' icon, select the next best distribution in the left-hand-side list. Parameters and Objects for the remaining four best-fitting distributions can be placed in the following cells:

2) PolyA - Parameters in R6:S7, Object in U7

3) NegBin- Parameters in R8:S9, Object in U9

4) BetaNegBin - parameters in R10:T11, Object in U11

5) BetaBinomial - parameters in R12:T13, Object in U13

After these five sets of parameters and Objects have been created, select "OK" to exit distribution-fitting window.

The final touch is to create cells that behave like uncertain input variables in Excel. We place the VoseSimulate function into the model architecture (input) and refer back to the fitted-distribution Objects.

• Select Cell P5.
• Type in "=VoseSimulate(U5)" and hit ENTER. (Or use Formula Bar tool to do the same).
• Copy Cell P5.
• Paste the formula into Cells P7, P9, P11, and P13.

We leave it to the reader to complete the exercise for the Opponent's Score in the rows directly beneath.

(After entering the MR enablers in Column P, single trials can be experienced if automatic recalculation is "on" in Excel (via Excel Options) and any changes are made elsewhere in the sheet. Try it out by typing a number in any blank cell and hitting ENTER.)

What becomes apparent immediately, in the ModelRisk world, is that we have a lot more options available for distribution-fitting. And do we, as self-appointed basketball experts, believe that these new alternatives are perhaps even better offerings than what Crystal Ball provided?

 

We do. PolyA is a modification of Poisson. Even better, PolyA substitutes the Gamma distribution (defined by two parameters) for the Rate parameter, allowing us to be uncertain about the actual scoring rate mean for each game. Perfect! Also helpful is Delaporte. It takes the PolyA modification of the Poisson even further, combining a static element (Rate) with an uncertain one (Gamma distribution & its two parameters) and subs that in for the Poisson Rate parameter. Also interesting are the Beta Negative Binomial and Beta Binomial. As you would suspect, they are modifications of the Binomial and Negative Binomial. Just like the Gamma distribution was used in Poisson, the Beta distribution is subbed in for the Probability parameter, placing uncertainty around the coin flip probabilities from game to game.

These are not the only reasons to be excited about discrete distribution fitting in MR. Another great bonus over CB fitting is that the data need not be static. There is no automatic feature in CB that updates CB Assumptions fitted to that data. The fitting operation needs to be manually run again to obtain a new set of PDF parameters. In MR, the user just needs to insert extra cells in the data ranges and all appropriate Vose formulas are updated, just like with Excel formulas. Voila!

Lastly, it should be mentioned that MR trumps CB in another important distribution-fitting category. MR allows the user to fit to the minimum number of samples necessary to calculate PDF MLEs. This can be a dangerous thing in the hands of a novice. MR guards against that danger by incorporating an uncertainty parameter in Vose functions. In contrast, CB places a minimum limit of 15 on the number of samples to be fitted. For those with frequent low number of samples, this is a major hindrance. We will return to this topic in the future.

There is one important tweak we have not placed on either of our CB or MR entities. Now we turn our attention to the added complication of correlations.