As with Crystal Ball, ModelRisk has the ability to fit distributions to historical data. The analyst looking to describe the variation of a Monte Carlo Analysis input can use "fitting" windows to select data and manipulate other options. How does the ModelRisk (MR) fitting experience stack up against the Crystal Ball (CB) methods and options? There are some important differences one should understand about MR before fitting PDFs to the Duke 09_10 Scores spreadsheet.

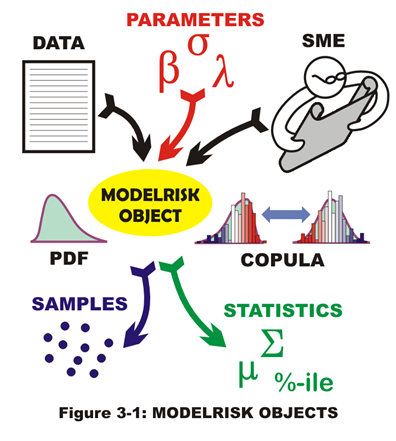
An important concept to embrace when using MR is that distributions or PDFs can be defined by magical entities called Objects. (They can also be defined directly by MR functions. However, there is greater power in defining them as MR Objects.) Objects are nothing new to the programming world. Objects have Properties that can be extracted from the Object itself. For instance, the parameters or percentiles of a PDF can be extracted from the PDF Object. The Object can be manipulated by fitting data or by defining the parameters explicitly. MR Distribution Objects are fundamentally different from CB Assumptions in how they behave and work in the MCA spreadsheet framework.

In CB, the Assumption is "layered" invisibly above or on the spreadsheet cell. When not running a simulation, the cell (colored bright green) will display the Base Case value inserted before the Assumption was created. (It cannot be a formula since it is an input.) During simulation, this value is ignored and only samples from the PDF are displayed while Excel calculates the outputs on each and every trial. Afterwards, the cell value returns to its Base Case value.

In contrast, the MR Distribution Object should reside in a separate cell, not layered invisibly over the input cell connected to the spreadsheet logic. The MR Object is then referred to by another cell which is connected to the spreadsheet mathematical model as an input (usually with the VoseSimulate function). The user can create many connections between the spreadsheet logic (the mathematical model portion of interest) and the MR Object to extract parameters, percentiles and randomly-generated values during simulation. For instance, if the same PDF is used multiple times in the same transfer function (analogous to two ball bearings from same manufacturer used in a one-way clutch assembly), the user needs to create the MR Object for the bearing PDF once (and only once) but then refer to that object (via VoseSimulate function) in two separate cells that are inputs in the transfer function of concern.

The CB Assumption (as with other CB entities) is not an Object, as such. Instead, it resides in a hidden worksheet within your Excel workbook and is created, manipulated, modified, etc… via the CB ribbon bar commands. It cannot be modified or entered directly in the spreadsheet cell formulas. (To counter that, CB does have functions analogous to those entered in MR and other MCA spreadsheet add-ins. However, they are not as powerful or flexible as those in other codes nor are there ones that do distribution-fitting.)

Whether this appeals to the user is a matter of personal preference. Analytical types will appreciate the power of manipulating MR formulas directly in the cell and have no issues in organizing their MR Objects within the spreadsheet. Others would rather work through a user-friendly interface to do the same, leaving less opportunity to "mess up" with tricky formulas. MR has capability of entering MR Vose functions directly or via user-friendly window; CB only has the latter. With this distinction in mind, let us now fit discrete distributions to data using ModelRisk.