
In this article, we are going to cover aspects of Monte Carlo tools which we believe will interest many readers – speed, accuracy and precision. We look at both dimensions of speed, development speed and numerical processing speed. Speeding up an analytics cycle-time to an answer is both about the time to model and the time to insight.
Picking the Candidates
The official release of the Julia Language which many consider to be the up and coming language to rival both R and Python, prompted this analysis. We have been keeping a close watch on Julia since 2014 because of the promises of ease and speed. Given that the language was still in beta we wanted to see if it would take. Now we are confident enough to have spent weeks going through the process of learning and benchmarking Julia against R, @RISK and Oracle Crystal Ball. We had considered Python because we feel it’s a solid platform with lots of packages and can perform well when combined with Numba, however we were not a able to get this contribution in before publishing but we will revisit in our next study.
In the 8 years that have passed we have seen many things change and others stay the same in the risk and decision modeling software space. Though @RISK and Crystal ball have had many releases since our first NFS (Need for Speed) comparison study, only in recent years has 64bit versions of all the tools tested become available. This time around we only tested correlated models (assuming that anything less is not useful) and focused on simulating returns using Normal Distributions in 64bit environments. Of course, we could have also tested distribution fitting but that could distort the results, so we left that out also. What we did focus on what the consistency of results and the time it takes to build a reliable solution.
Comparing Excel and Code approaches to simulation
It goes without saying that coding a simulation model and developing one in Excel with advanced add-ins that both automate and simplify the Monte-Carlo modeling process are indeed two very different undertakings. Basically it’s a trade-off between development time and the time it take to update the inputs and run again (automation into the business process). Coding a solution can take 10-15x more time to develop than it’s equivalent Excel counterpart but deliver run times and the ability update and refresh inputs automatically making the coded solution 100x – 10000X faster on the back end.
Given that many of our clients are seeking to leverage/share existing models and put them in broad use, we need to identify a language that was practical, fast, intuitive to code and easy to read. Another core consideration is that it needed to be a natural evolution for someone who is proficient in Microsoft Excel and VBA because again, we often get the question : “What language should I learn if I know Excel VBA?”. So in this review, we consider both Julia and R as counters to Excel.
Methodology
Testing for accuracy & precision
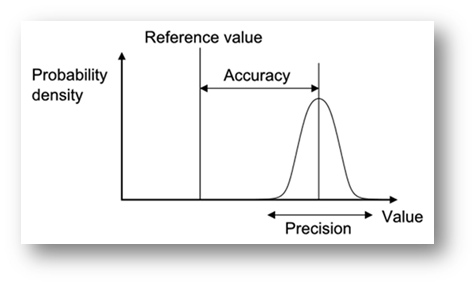
In order to test for accuracy we averaged out the values of all 20 simulations for each percentile/package and compared the results against the calculated form using the Markowitz mean variance approach. As for precision, we looked at the error (theoretical minus simulated results) of each percentile/package at a given number of trials for all 20 simulations. For example, we would look at the standard deviation at the 99th percentile using a sample of 20 simulations at 10,000 trials each (200,000 trials total). Our basic objective when analyzing a package for precision is whether it follows a certain set of statistical rules. A good example would be the expectation for a reduction of standard deviation as we increase the number of trials at a given percentile. When we set up the script to test the accuracy of each tool we realized that it would be easy to do a performance comparison as well. This turned out to be an added bonus! During the scripted tests, we also took into account the execution time of the whole script and that of each simulation. We also evaluated the average trials/sec for both the test and the individual simulations.
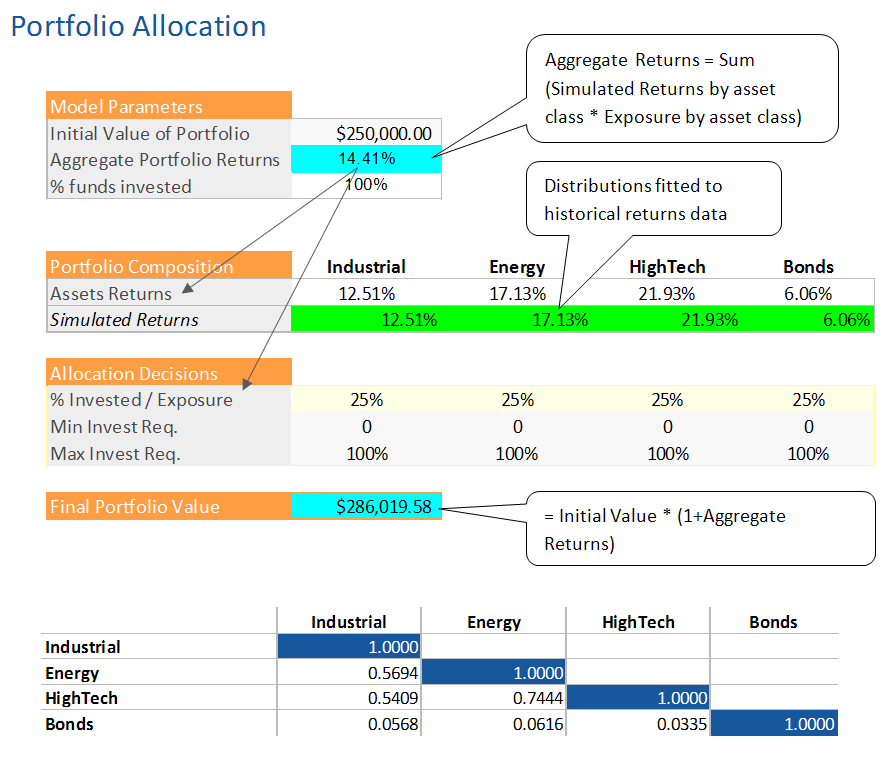
Test model for benchmarking development and run times
An investor seeks to evaluate the risk in his portfolio. We have $250,000 to invest and must make sure we have a better chance at making money than losing it. For purposes of the exercise, we are using the Markowitz Modern Portfolio Theory (1952) and allocated our investment equally among each asset class at 25% a piece. We analyzed the rank correlation (using the Excel based method presented Copulas vs. Correlation) and prepared a correlation matrix that was used to correlate the returns distributions for each class. In Julia, we replicated all of the logic from Excel and it’s add-ins, including the use of the Iman-Connover (1982) correlation algorithm to correlate the assets together.
Test Environment
Our test machine consisted of a Dell Precision T7600 system with Dual Xeon Processors with a total of 12 cores, 16 GB of RAM, Windows 10 and Microsoft Office 365. A few notes on the test environment and simulation in general:
- Most applications are single threaded. That means that one worker process runs on one processor core. For example, on a machine with 12 cores, you will get a max of 1/12 of your processor capacity. In general fewer but bigger cores make a big difference. The I series by Intel makes good use of this.
- All the applications were tested in their 64bit versions.
- Though Extreme Speed was deprecated in Crystal Ball 11.1.2.4.8, we have included the results for indicative reasons. We tested both CRAN and MRAN versions of R.
Speed Summary
What about Accuracy, Precision and all the other findings?