In the case of the one-way clutch example, the current MC quality prediction for system outputs provide us with approximately 3- and 6-sigma capabilities (Z-scores). What if a sigma score of three is not good enough? What does the design engineer do to the input standard deviations to comply with a 6 sigma directive?

Both RSS and MC analysis provide information on Sensitivity Contributions. (WCA does not.) These contributions are reported as percentages whose total from all input contributions must equal unity (100%). If an engineer knows that some inputs contribute more (or even way more) to variation output than others, would that be of use? Absolutely. Then a plan can be formulated to attack those inputs driving quality (if possible) and pay less scrutiny to the others.

Figure 12-1 displays Sensitivity Charts produced from a CB simulation. From these charts we can visually gage the percentage contributions. Note that the absolute value sum of the contributions equals 100%. At the same time, some input contributions are displayed as negatively contributing while others are positive. It does not mean the percentages are negative. However, they do provide information about the sign (plus or minus) associated with the input sensitivity (also known as the slope or 1^st derivative). This relays other design information to the engineer. Namely, how would the output mean be shifted (up or down, negative or positive) if an input mean shifted. These values are to be compared with the RSS sensitivity contribution results. Are MC and RSS in agreement on the predicted input contributions?

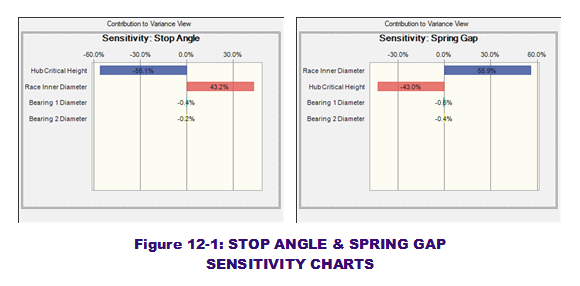
For the one-way clutch example, they do a pretty good job as shown in the following two tables:

(As an aside, note that I have listed only one total contribution associated with Bearing Diameter whereas the Sensitivity Charts indicates there are two, one for each separate bearing. In order to compare our previous RSS results, I have summed the two MC bearing contributions. As always, your results may vary depending on number of trials and seed value.)

Now the design engineer's mission is clear. The Hub Critical Height wins out over Cage Inner Diameter in contribution percentage. What can be done to control its variation tighter than currently estimated? What if the machining process that makes the hub cannot provide any tighter variation? In that case, the engineer focuses on what can be done on Cage Inner Diameter, which is a purchased part. But placing any more effort on tightening Bearing Diameter variation would be a waste of time. Sensitivity Analysis in a Tolerance context has great power. It shows the way forward to addressing a quality problem.

Let us summarize the three methods and their pros and cons in the post to follow.

Creveling, Clyde M., Tolerance Design: A Handbook for Developing Optimal Specifications (1997); Addison Wesley Longman, pp. 172-175.

Sleeper, Andrew D., Six Sigma Distribution Modeling (2006); McGraw-Hill, pp. 122-124.